Representación de triángulos

Triángulo conocidos los tres lados

Triángulo lados y ángulo comprendido

Construcción de un triángulo dado un lado y dos ángulos

Autoevaluación por parejas

¿Qué te ha parecido el examen por parejas?.
   La verdad es que me ha parecido una buena manera de aprender de mis errores, es decir, gracias a esta prueba me doy cuenta de que tengo fallos en donde yo pensaba que no tenía.
¿Has aprendido algo nuevo mientras lo hacías?¿Qué?
   Este examen me ha puesto a prueba a la hora de controlar el tiempo e intentar organizarlo lo mejor posible.
¿Que te ha parecido trabajar con la pareja elegida?
 Me ha parecido que hemos estado bastante bien en cuanto a trabajo, los dos hemos trabajado lo mismo y casi teníamos el mismo nivel de conocimientos.
  ¿Estaban ajustadas las preguntas a lo que habíamos trabajado en clase?
   Las preguntas estaban totalmente ajustadas, ya habían sido trabajadas en clase, no había trampa.
¿Les dió tiempo,que quitarías/añadirías...
  Nos faltó un poco de tiempo ya que no nos organizamos bien a la hora de hacer los ejercicios, nos reparamos mucho en uno de ellos.
Gracias a esta autoevaluación nos hemos dado cuenta de fallos tan garrafales que ni nosotros mismos sabíamos que podíamos cometer, pero que difícilmente cometeremos otra vez.

Temario de primero de bachillerato

Números reales.

Este curso hemos empezado con un tema que se ha machacado a lo largo de toda nuestra historia académica ,por lo que es un tema que hay que tenerlo bastante bien dominado.
  En primer lugar conoceremos cómo clasificarlos con un esquema visual que nos facilitará su aprendizaje.

Los números reales son aquel conjunto compuesto por los racionales e irracionales. Dentro de los racionales podemos encontrarnos a los naturales, que son aquellos números positivos y no decimales, a continuación se encuentran los números enteros que comprenden todos los números positivos y negativos no decimales y por último los racionales fraccionarios que consisten en todos los números decimales, periódicos. Por otra parte, tenemos los irracionales que son aquellos que presentan una infinita cantidad de decimales.

Notación científica

¿Qué es? Es simplemente una forma de facilitarnos la lectura y escritura de números con valores muy altos a través de una potencia de diez, es decir:

Como se puede ver en ejemplo, para expresar algún número muy pequeño solo debemos aplicar el mismo criterio que a los grandes con la diferencia de que la potencia será negativa. Cabe destacar que en este tipo de notación, en la parte entera del número no puede haber más de una cifra.

Sumas y restas en notación científica.

Para realizar estas operaciones es necesario que nuestras potencias de diez presenten el mismo exponente, sin importar que nuestra parte real del número supere más de una cifra. A continuación se opera como hemos acostumbrado:

Multiplicación y división

Para multiplicar dos números en notación científica simplemente multiplicamos los coeficientes que forman los números, luego copiamos la base y sumamos los exponentes.

Si ax10^b es un número en notación científica y cx10^d es otro número expresado en notación científica entonces el producto de estos dos números es:

(a x 10^b) · (c x 10^d) = a·c x 10^b+d

Entornos:

En este apartado del tema he pensado que lo mejor sería exponer un pequeño video que lo explicase ya que en su momento no puede entenderlo de una manera óptima por lo que no sabría si me estaría expresando de una manera adecuada al explicarlo con mis palabras. Como siempre recurrimos a nuestro querido unicoos ;).

Aproximaciones y errores

Aproximaciones

En ocasiones, ciertos números tales como   π,  √2,  5,675...   dificultan el trabajo.
En estos casos usamos valores próximos a dichos números para simplificar los cálculos.
Es por ello que surgen los siguientes conceptos:

Aproximación por defecto o truncamiento

Consiste en eliminar las cifras a partir del orden considerado.

Aproximación por exceso

Se eliminan las cifras a partir del orden considerado, pero se aumenta en una unidad la última cifra que dejamos.

Redondeo

Es la mejor de las aproximaciones de las dos anteriores.

Se aumenta una unidad si el decimal útimo está comprendido entre 5 y 9.
Y se deja igual si está comprendido ente 1 y 5.

	Aproximación por defecto o truncamiento	Aproximación por exceso	Redondeo
5,357	5,35	5,36	5,36
	7,33	7,34	7,33
	1,73	1,74	1,73
	1,02	1,03	1,03

Errores

Error absoluto

Es la diferencia, en valor absoluto, entre el valor real y la aproximación.

Error relativo

Es el cociente del error absoluto y error real.

Ejemplos de error absoluto y error relativo:

Calcular los errores cometidos al redondear 5,327 a las centésimas.

5,327   redondeo a la centésima →   5,33

He decidido escoger la información de esta página porque me parece que está muy completa ya que aunque parezca que no este apartado tiene que ser entendido muy bien para no cometer errores a la hora de aplicarlo a ejercicios:http://calculo.cc/N%C3%BAmeros_reales/Aproximaciones_y_errores.htm

                                                     Logaritmos

La definición más acertada pero a la vez más difícil de entender es la siguiente:

En análisis matemático, usualmente, el logaritmo de un número real positivo —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10³ = 10×10×10.

Su definición expresada algebráicamente sería la siguiente:

Hay distintos tipos de logaritmos: aquellos de base diez y los logaritmos neperianos que aunque no vaya a profundizar, son aquellos con base el número "e".

Es cierto que al principio cueste un poco pero la verdad es que aprendiendo las siguientes propiedades de los logaritmos tengas más del 90% de tus dudas resueltas.

Esta imagen en cuanto a las operaciones con los logarítmos pero...¿que podemos hacer cuando se trata de una ecuación logarítmica?

Los números complejos

¿Qué son?

Son aquellos números cuyo cuadrado es negativo, pero espera, ¿Esto no es imposible? Desde que una serie de matemáticos propusieran los números imaginarios no. Gracias a este descubrimiento hemos podido resolver aquellas malditas ecuaciones que acababan en una raíz de un número negativo. 

En esta siguiente imagen podemos apreciar las diferentes partes de un número complejo expresado en forma binómica.

En la siguiente podemos apreciar la forma polar de dichos números:

Estas dos formas de los números pueden ser representadas por la otra, es decir la binómica en polar y viceversa, para pasar de forma binómica a polar:

Y de polar a binómica:

Teniendo en cuenta lo anteriormente hablado podemos pasar a las operaciones con estos números que son muy parecidas a la de los números reales.

La división es muy parecida a la racionalización de denominadores.

Triángulo de Tartaglia

El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito                                                                                                                        1

    1    1
    1    2    1
   1    3    3    1
   1    4    6    4    1
   1   5   10  10    5   1

   ...........................

El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy anterior al de estos dos matemáticos . Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII).

Este triángulo nos sirve para resolver potencias de un número complejo en forma binómica; esto es mejor que sea explicado por un video ya que requiere de bastante comprensión:

• ¿Qué es lo más importante que he aprendido con esta Unidad y durante el tiempo en el que transcurrió?
• Para mí lo más importante han sido los números complejos entre las unidades impartidas. Parece ser que puede resolver problemas que sin ellos sería imposible. A parte de esto son muy interesantes.
• ¿Qué preguntas, dudas o dificultades se me plantean?
• Las dudas que más me frecuentaron en mi mente de estudiante adolescente fueron con respecto a la aproximación y cota de errores, aunque parezca mentira. Otro tema que me mantuvo noches en vilo fue el triángulo de tartaglia que por mucho que intentara resolver ejercicios con este, era imposible para mí.
• ¿Qué consecuencias tiene lo aprendido con mi vida, a nivel personal y académico?
• A nivel académico lo que más me servirá serán las aproximaciones y sobre todo las aproximaciones y errores ya que mi objetivo es estudiar ingeniería. En mi opinión a nivel personal y de la vida de poco va a servir aunque eso no quiere decir que no sea bueno o necesario aprenderlo.
• ¿Para qué me sirve? ¡Qué puedo hacer yo con ello?
• Con ello lo máximo que haré será prepararme para la carrera anteriormente mencionada.

Opinión del curso

En esta entrada voy a intentar compartir mi experiencia a lo largo del curso en la asignatura de matemáticas.
   Voy a empezar por el principio, trigonometría. En su momento me parecía un tema que no iba a terminar de comprender nunca pero ya a finales de curso, usándolo en física, fue cuando comprendí sus usos y lo comprensible que era esta tema...
  Si no me equivoco, el segundo tema impartido en el primer trimestre fue el relacionado con los polinomios, en este apartado estudiamos la factorización de los mismos, a través de ruffini y otros métodos que se pueden encontrar en mi blog. En mi opinión fue una materia no dificil pero si que ha de ser trabajada para su completa comprensión.
   A medida que pasaba el curso nos íbamos adentrando en uno de los asuntos que más suele costar a los alumnos, las ecuaciones. Impartimos de primer y segundo grado, completas e incompletas, inecuaciones, bicuadráticas y sistemas de ecuaciones. Este tópico es muy mecánico y a medida que vas empleando tus conocimientos aprendidos durante el curso y vas practicando le vas cogiendo el "tranquillo" al álgebra.
    Aquí llega el tema que más me ha costado entender (todavía no lo comprendo del todo) de todo el curso, las funciones.
     En este temario impartimos varias funciones como las rectas, parábolas, de proporcionalidad inversa, exponenciales y a trozos. La verdad es que me gusta el uso de las funciones pero no logro comprender su representación e identificación.

Proporcionalidad inversa

Esta vez voy a repetir mi entrada de proporcionalidad inversa ya que la otra no me había salido bien, en este caso voy a recurrir a Fausto de nuevo, es una fuente inmensa de parábolas...

Para realizar esto, como el nombre de la función indica, se necesita invertir algo. En este caso se invierte un número (x) y a partir de ahí se le puede sumar o restar lo que se desea a dicha función. Espero que en esta entrada quede más claro.

Proporcionalidad inversa

Esta vez les traigo una imagen con pequeñas muestras de proporcionalidad inversa

Parábolas y rectas

Parábolas y rectas

En estos últimos días antes de semana santa, estuvimos dando en clase un nuevo tema interesante que son las rectas y parábolas. Las parábolas ya las he publicado en una entrada, ahora toca hablar sobre las recta.La palabra recta se usa para dar cuenta de todo aquello o aquel que se dirige a un punto sin desviarse y que por lo tanto en su trayectoria no se inclina hacia los dos lados, no presenta ni curvas ni ángulos.
Ya sabiendo lo que es, procedamos a aplicarlo en geogebra:

En esta imagen se puede mostrar la aplicación de dichas rectas, su función se resume en un número que multiplica a X que define la inclinación más otro que indica la posición en el eje X.

Contenidos estudiados de álgebra

En esta ocasión traigo un pequeño repaso de todo lo que hemos aprendido de álgebra:

   Índice:
    -Monomios: definición y resolución de ejercicios sencillos.
    -Polinomios: operaciones,identidades notables, ruffini, teorema del resto y factorización.
    -Ecuaciones: segundo grado,incompletas ,completas ,bicuadradas ,irracionales y sistemas.
    -Inecuaciones.
    

Monomios: son las expresiones más sencillas y están formadas por una parte numérica llamada coeficiente (cuando es 1 se suprime) y una parte literal formada por una letra elevada a un exponente natural (o el producto de varias de estas potencias). De esta forma, las dos expresiones anteriores se corresponden a monomios.

Así por ejemplo, en el monomio 15x2 , el coeficiente es 15 y la parte literal es x2 .

En el monomio x3, el coeficiente es 1 y la parte literal es x3 .

También se considerará como un monomio a aquel que sólo tiene parte numérica. De esta forma, 8 por ejemplo, sería un monomio. Cuando forma parte de otra expresión más compleja, como por ejemplo 2x + 8 , diremos que es el término independiente.

Dos monomios son semejantes si tienen la misma parte literal:

      -   8x2 , -5x2 , x2 son monomios semejantes (todos tienen la misma parte literalx2)

      -   3xy4, -2xy4 son monomios semejantes (todos tienen la misma parte literal xy4 )

      -   x2  y 7x3 , no son semejantes ya que en el primero su parte literal es x2 y en el otro x3 (son diferentes).

     Aquí les dejo unos ejercicios como ejemplos.
         

Polinomios

Las expresiones algebraicas que se forman a partir de la unión de dos o más variables y constantes, vinculadas a través de operaciones de multiplicación, resta o suma, reciben el nombre de polinomios.

Para calcular la suma de los polinomios:

(4x4 - 2x3 + 3x2 - 2x + 5 ) + ( 5x3 - x2 + 2x )

Basta sumar los términos de grados 3, 2 y 1 de ambos polinomios y dejar el resto de los términos del primero como está.

Podemos indicar la suma de la siguiente forma para verla mejor:

4x4 - 2x3 + 3x2 - 2x + 5

+ --- 5x3 --- x2 +2x

_____________________

4x4 + 3x3 + 2x2 + -----5

Por tanto: Para sumar dos o más polinomios se suman los términos semejantes de cada uno de ellos.

Si en lugar de sumar dos polinomios se tratara de restarlos, bastaría cambiar el signo a todos los términos del segundo y sumar los resultados.

Para dividir polinomios:

Con los polinomios dividendo y divisor ordenados de mayor a menor grado:

- Se divide el primer término del dividendo entre el primero del divisor, dando lugar al primer término del cociente

- Se multiplica dicho término por el divisor y se coloca debajo del dividendo con los signos contrarios, cuidando que debajo de cada término se coloque otro semejante

- Se suman los polinomios colocados al efecto, obteniéndose un polinomio de grado menor al inicial

- Se continua el proceso hasta que el resto ya no se pueda dividir entre el divisor por ser de menor grado.

Normalmente se dividen polinomios con una sola variable (x) tanto en el dividendo como en el divisor.

Multiplicación de polinomios

Para multiplicar dos polinomios se multiplican los términos del primero por cada uno de los del segundo y se reducen los términos semejantes.

R(x) = 5x3 + x - 1

S(x) = 2x2 - 1

R(x) · S(x) = (5x3 + x - 1) · (2x2 - 1) =

=(5x3) · (2x2) + (5x3) · (-1) + (x) · (2x2) + (x) · (-1) + (-1) · (2x2) + (-1) · (-1) =

=10x5 - 5x3 + 2x3 - x - 2x2 + 1 = 10x5 - 3x3 - 2x2 - x + 1

Identidades notables 

Las identidades notables son varias expresiones algebraicas

Binomio al cuadrado

El binomio al cuadrado es una de las identidades notables más típicas y que a pesar de ello, muchas veces se resuelve mal.

Estas son las fórmulas que hay que aplicar para resolver una identidad notable de un binomio al cuadrado:

(a + b)2 = a2 + 2ab + b2

(a − b)2 = a2 − 2ab + b2

Los términos que se elevan al cuadrado siempre van con un signo positivo mientras que el término que es igual al doble del primero por el segundo tendrá un signo que será positivo o negativo dependiendo del que haya en la identidad notable.
Ejercicios resueltos:

(x + 2)2 = x2 + 4x + 4

(x – 2)2 = x2 – 4x + 4

Suma por diferencia

Cuando aprendemos la identidad notable de la suma por diferencia nos enseñan que es igual a la diferencia de cuadrados. Esto se resume en la siguiente fórmula:

(a + b) (a − b) = a2 − b2

Lo siguiente es ruffini.

El método o regla de Ruffini es un método que nos permite dividir un polinomio entre un binomio y además permite localizar las raíces de un polinomio para factor izarlo en binomios.
En otras palabras esta técnica posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1. Y para que esto sea posible se necesita saber o conocer por lo menos una de las raíces del polinomio único, con el propósito de que la separación sea exacta.

Se deben colocar todos los coeficientes del dividendo ordenados de mayor a menor grado y si falta el de algún grado intermedio colocar un 0.

           Teorema del resto:

Teorema del Resto: El resto de dividir el polinomio P(x) entre el monomio a x − es igual al valor numérico del polinomio para a x = , es decir P(a). 

Para factorizar polinomios, he decidido no dejar explicación, sino publicar los siguientes vídeos:

Ahora viene el apartado que más me cuesta de todos, las ecuaciones.

En matemática se llama ecuación a la igualdad entre dos expresiones algebraicas, que serán denominados miembros de la ecuación. En las ecuaciones, aparecerán relacionados a través de operaciones matemáticas, números y letras (incógnitas).

-Para resolver ecuaciones de primer grado con una incógnita, seguimos los siguientes pasos:

-Quitar paréntesis (si los hubiese)

-Quitar denominadores (si los hubiese)

-Transposición de términos: colocar los términos con incógnita en un miembro y los que no tienen incógnita en el otro miembro (para ello usamos la Regla de la suma)

-Agrupar términos: Sumamos en cada miembro los términos semejantes (ver Suma de monomios)

-Despejar la incógnita: para ello usamos la Regla del producto

-simplificar el resultado: en la mayoría de ocasiones deberemos simplificar la fracción resultante

Ejemplos:

Ecuaciones de segundo grado:

-Ecuación Completa: se dice que una ecuación de segundo grado del tipo  es completa cuando los coeficientes b y c  son distintos de 0.

-Ecuación Incompleta: se dice que una ecuación de segundo grado del tipo  es incompleta cuando alguno                                                                                                      de los coeficientes b y c  son iguales a  0.          

-Las ecuaciones de segundo grado incompletas son aquellas en las que faltan las constantes b o c o incluso las dos, es decir, que son igual a 0. Tenemos 3 tipos:

Cuando b=0: ecuacion de segundo grado incompleta 2

Cuando c=0:ecuacion de segundo grado incompleta 1

Cuando b = 0 y c = 0:ecuacion de segundo grado incompleta 3

Aquí les dejo una ilustración para que quede más claro:

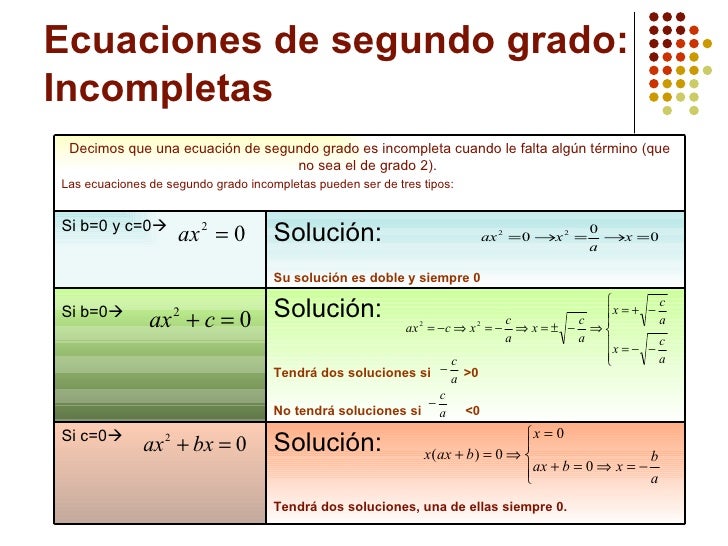
Y ahora las completas:

Ecuaciones bicuadradas (de las más sencillas para mí).

Por ecuaciones bicuadradas nos referimos a las ecuaciones de grado 4 que tienen la siguiente forma:

ax^4+bx^2+c = 0

Para resolver este tipo de ecuaciones, vamos a hacer un cambio de variable:

t=x^2

Y sustituimos cada x^2 por una t quedando la ecuación de la siguiente forma:

at^2+bt+c=0

Se resuelve mediante la fórmula de las ecuaciones de segundo grado obteniendo dos soluciones que llamaremos t_1 y t_2,estas ecuaciones son casi iguales que las de segundo grado con la diferencia que hay que cambiar la variable.

Con radicales (no las controlo en estos momentos).

Aquí les dejo una información muy bien explicada (para mí) de como resolverlas:

Método de Resolución

Vamos a explicar el método de resolución a través de un ejemplo:

$$\sqrt{x-1}-1=0$$

1. Reordenamos la ecuación: aislamos la raíz en uno de los lados:
   
   $$\sqrt{x-1}=1$$
2. Elevamos ambos lados al orden de la raíz. Si la raíz es cuadrada, elevamos a 2; si es cúbica, elevamos a 3; si es de orden 4, elevamos a 4...
   
   $$(\sqrt{x-1}{)}^2=1^2$$
3. Desarrollamos las potencias. En nuestro ejemplo, el signo radical desaparece y el cuadrado de 1 es 1:
   
   $$x-1=1$$
4. Si quedan raíces, vamos de nuevo al primer paso. Si no quedan raíces, resolvemos la ecuación:
   
   $$x-1=1$$
   $$x=1+1$$
   $$x=2$$
5. Comprobamos que todos los radicandos son positivos para las soluciones obtenidas:
   Nuestro radicando es
   
   $$x-1$$
   Sustituimos x = 2 :
   
   $$x-1=2-1=1>0$$
   Si alguna de las soluciones hace que el radicando sea negativo, entonces no es una solución.
6. 
   

Si alguna de las soluciones hace que el radicando sea negativo, entonces no es una solución.

Por si no les ha quedado claro, les adjunto un pequeño vídeo de nuestro querido "unicoos".

Ahora, pasemos con los sistemas:

Esta es una información que he encontrado por google que es muy buena, si les interesa la página, se llama: https://bitacoraed.wordpress.com

• Método de sustitución

  Es aconsejable en sistemas en los que aparecen coeficientes  o .
  
  1. Despejamos la  de la primera ecuación: 
  2. Sustituimos en la otra ecuación:
  3. Resolvemos la ecuación resultante:
     
     
     
  4. Para averiguar el valor de  sustituimos el valor de  en la expresión obtenida el el paso 1
     
     

• Método de igualación

  
  1. Despejamos la misma variable de ambas ecuaciones
     
     
  2. Igualamos las dos expresiones anteriores
     
  3. Resolvemos la ecuación resultante
     
     
     
  4. Para calcular el valor de x sustituimos  en cualquiera de las expresiones obtenidas en el paso 1
     

• Método de reducción

  Combinación lineal de ecuaciones : se multiplica una ecuación por ún número, la otra por otro número y se suman. La ecuación resultante de una combinación lineal es equivalente a las ecuaciones originales del sistema.
  El método de reducción consiste en eliminar una incognita del sistema.
  
  1. Vamos a eliminar la . Para ello multiplico la ecuación de arriba por 3 y la de abajo por 2:
     
  2. Sumando ambas ecuaciones desapacen las x y nos queda
     
     
  3. Para calcular x sustituimos en cualquiera de las ecuaciones originales. Sustituyendo en la primera nos queda
     
     
     

Y por último un tipo de sistema que es el no lineal:

Este es el proceso:

-En primer lugar se despeja una de las dos incógnitas

-En segundo lugar ,con la incógnita despejada, se sustituye

-En tercer lugar se opera y se unen "peras con peras y manzanas con manzanas"

-Y se realiza la ecuación de segundo grado mediante su fórmula carácterística

-Por último con una de las incógnitas despejadas se sustituye para averiguar la otra

Inecuaciones:

Una inecuación es una desigualdad que relaciona letras y números mediante las operaciones aritméticas. Las letras se llaman incógnitas. Las soluciones de una inecuación son los valores que pueden tomar las incógnitas de manera que al sustituirlos en la inecuación hacen que la desigualdad sea cierta.

Procedimiento para resolver una inecuación de primer grado con una incógnita.

 • Quitar denominadores, multiplicando ambas partes de la inecuación por el mínimo común múltiplo de los denominadores (propiedad 2 o 3). 

• Quitar paréntesis. (propiedad distributiva). 

• Transposición de términos, para conseguir una inecuación de una de las formas siguientes: a ⋅ x < b , a ⋅ x ≤ b , a ⋅ x > b , o bien a ⋅ x ≥ b (propiedad 1) • Despejar la incógnita. (Propiedad 2 o 3)

 • Determinar la expresión analítica, por intervalos y gráfica de la solución. 

Bueno, eso es todo, espero que esta publicación les ayude a aprobar mates ;).