1¿Qué es la trigonometría?
2 Reducción al primer cuadrante y radianes.
3 Resolución de triángulos a través del teorema del seno y el coseno.
4 Ecuaciones e identidades trigonométricas.
5 Reflexión sobre el tema.
1¿Qué es la trigonometría?
La trigonometría es la subdivisión de las matemáticas que se encarga de calcular los elementos de los triángulos. Para esto se dedica a estudiar las relaciones entre los ángulos y los lados de los triángulos.
Esta especialidad interviene en diversas áreas de las matemáticas en las que se necesita trabajar con precisión. La trigonometría, de todas formas, cuenta con una amplia variedad de aplicaciones. Permite, por ejemplo, medir las distancias entre dos ubicaciones o cuerpos celestes a partir de técnicas de triangulación. La trigonometría también se aplica en los sistemas de navegación satelital.
2 Reducción al primer cuadrante
Un ángulo puede estar situado en cualquiera de los cuatro cuadrantes de la circunferencia. Los valores de sus correspondientes razones trigonométricas dependen de su posición.
Cuando un ángulo se encuentra situado en el segundo, tercero o cuarto cuadrante siempre es posible relacionarlo con otro del primer cuadrante cuyas líneas trigonométricas tengan los mismos valores absolutos.
Las relaciones entre las razones trigonométricas de los ángulos situados en los distintos cuadrantes resultaba esencial cuando no se disponía de calculadoras. Existían tablas con los valores de las razones para ángulos del primer cuadrante. Los demás ángulos no figuraban en la tabla pues no era necesario: bastaba con reducirlo al primer cuadrante.
Para reducir dichos ángulos al primer cuadrante simplemente nos hace falta el uso de algunas "fórmulas" que harán que calcular senos y cosenos sea más fácil:
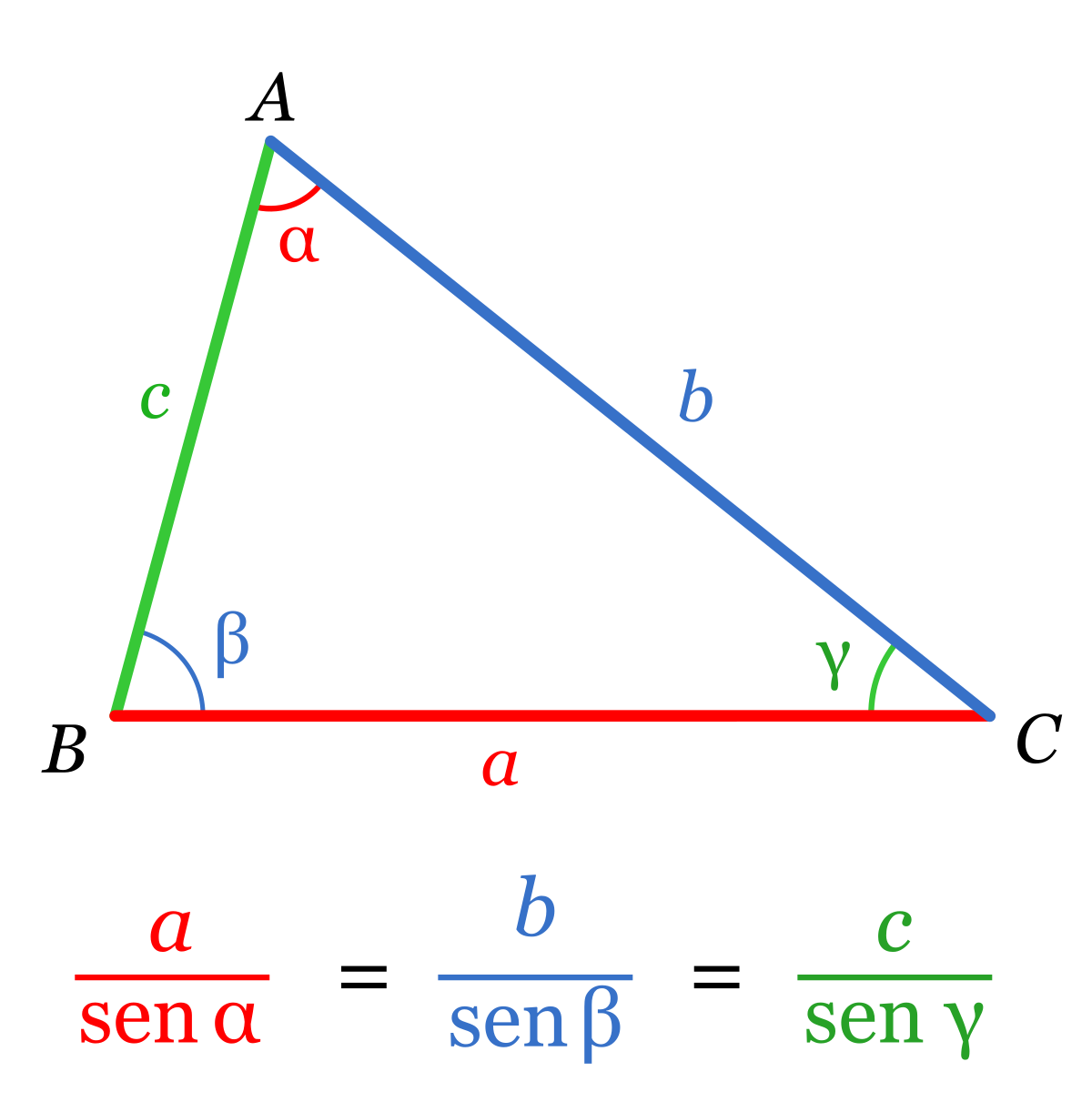
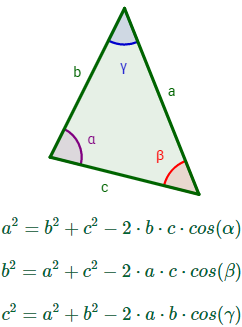
3 Resolución de triángulos a través del teorema del seno y el coseno.
Es aquí donde se pone en práctica la trigonometría, en el cálculo de triángulos.
Para resolver estos triángulos es necesario el uso de ciertas fórmulas adjuntas a continuación que serán empleadas según lo que estemos hallando.
4 Identidades trigonométricas y ecuaciones.
Es aquí donde la trigonometría se relaciona con el álgebra para lograr resolver algunos problemas.
Identidades trigonómetricas:
Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Ecuaciones trigonométricas
En estos ejercicios debemos hallar el valor de "x" que cumpla con las igualdades y proceder como una ecuación algebraíca normal.
5 Reflexión sobre mi evolución en el tema
¿Qué es lo más importante que he aprendido con esta Unidad y durante el tiempo en el que transcurrió?
Durante esta unidad he aprendido todo lo que he comentado anteriormente en esta entrada a parte de algunas maneras y trucos para hacer más sencillo el aprendizaje. Es muy importante para muchos oficios o carreras como la arquitectura.
¿Qué preguntas, dudas o dificultades se me plantean?
La dificultad más grande en mi caso era adquirir la concentración necesaria para no despistarme ya que soy propenso a equivocarme con signos y aspectos sencillos del tema.
¿Qué consecuencias tiene lo aprendido con mi vida, a nivel personal y académico?
A nivel personal significa aprender algo nuevo aunque no me interese demasiado .A nivel académico probablemente lo usaré en el curso que viene y sobre todo en la carrera a la que me matricularé.
¿Para qué me sirve?¿Qué puedo hacer yo con ello?
A nivel personal no creo que me sirva mucho pero gracias a estos conocimientos podré alcanzar cursos superiores e intentar llegar a lo que quiero ser en unos años.
“Cuando no tienen nitrógeno en el ambiente, una de cada diez se diferencia en un tipo de célula diferente que fija nitrógeno para todas las demás”, señala el científico. Lo que sorprende de este descubrimiento es que siempre siguen el mismo patrón, estas cianobacterias se dividen en filamentos de diez células y la última de esta fila es la que fija dicho nitrógeno. En mi opinión esto demuestra que las matemáticas no las hemos "creado" nosotros, sino que han existido siempre,lo único es que estaban cifradas en un código que no éramos capaces de descifrar, pero poco a poco hemos ido consiguiéndolo...
